Autómatas celulares
Autómatas celulares estocásticos logísticos
Un autómata celular estocástico (ACE) se caracteriza, y se diferencia de uno determinístico, por el hecho de que la regla de transición que gobierna el cambio entre estados de una célula es de naturaleza estocástica o probabilística.
Consideramos en esta sección el ACE logístico, que solo admite dos posibles estados para cada célula y cuya regla de transición local haremos depender de dos parámetros,  y
y 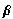 , y de los estados de las células vecinas durante la etapa anterior de la evolución.
, y de los estados de las células vecinas durante la etapa anterior de la evolución.
Supónganse k células alineadas sobre un segmento de recta a intervalos iguales, cada una de ellas susceptible de encontrarse en uno de dos estados posibles, que enumeramos por 0 y 1. Inicialmente, a cada célula se le asigna un estado, dando lugar a la configuración global inicial del ACE; diremos también que esta configuración corresponde a la etapa n = 0.
Las células van cambiando sus estados en los instantes sucesivos influenciadas por los estados de sus vecinas, las más cercanas a ellas, durante el instante anterior. Todas aquellas células que influyen sobre otra dada forman su vecindad. En el caso de los ACs cuyos elementos se encuentran alineados, es común establecer vecindades atendiendo al radio (r) de influencia; así, si r = 1, las células vecinas de la que ocupa la posición i son las que se encuentran a una distancia menor o igual a 1, que serán las posicionadas en i - 1, i e i + 1; y si r = 2, las vecinas de i serán i - 2, i - 1, i, i + 1 e i + 2.
Si se considera, por simplicidad, una vecindad de radio r = 1, y llamando xi n al estado en que se encuentra la celda i en el instante n, la probabilidad de que su próximo estado sea cero será
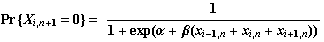 ;
; y
y 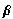 que se podrán ajustar a voluntad. Si esta es la probabilidad del suceso Xi, n+1= 0, la del suceso contrario será
que se podrán ajustar a voluntad. Si esta es la probabilidad del suceso Xi, n+1= 0, la del suceso contrario será
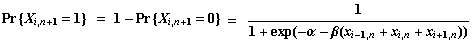 .
.
Con la definición anterior se establece una amplia familia de ACEs logísticos, sin más que ajustar los parámetros  y
y 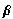 a dos números reales cualesquiera. Lo curioso de este modelo es que variando estos dos parámetros se observan comportamientos muy dispares; para cerciorarse de esto, basta con ensayar en el applet de esta sección con los ejemplos de la siguiente tabla o con otros valores del plano paramétrico. Se apreciará la riqueza dinámica de este modelo espacio-temporal.
a dos números reales cualesquiera. Lo curioso de este modelo es que variando estos dos parámetros se observan comportamientos muy dispares; para cerciorarse de esto, basta con ensayar en el applet de esta sección con los ejemplos de la siguiente tabla o con otros valores del plano paramétrico. Se apreciará la riqueza dinámica de este modelo espacio-temporal.
| Selección de pares paramétricos para radio de vecindad r = 1 | ||
| alfa | beta | Descripción |
| -8 | -5 | El comportamiento es tal que aun partiendo de una configuración inicial aleatoria el ACE alcanza estados globales homogéneos con todas, o casi todas, las células en estado 0 ó 1. |
| 2 | 5 | |
| 7 | -7 | Comportamiento claramente cíclico de periodo 2. |
| 0 | 0 | Caso extremo en el que anulando los parámetros se eliminan las interacciones; la dinámica es claramente aleatoria y uniforme. |
| 0 | -5 | Aunque haya desorden en las configuraciones, o bien dominan los estados en 1 ó en 0. |
| 7 | -2.6 | |
| -1 | 0.7 | Es la región más interesante del plano paramétrico, ya que la aparición de clústeres espacio-paramétricos sugiere la presencia de algún tipo de autoorganización a partir de las interacciones locales, fenómeno éste relativamente común en los ámbitos biológico y social. |
| -2.7 | 1.8 | |
| -4.5 | 3 | |
Nota: En este simulador, el tiempo transcurre de arriba hacia abajo, partiendo de una configuración inicial aleatoria, donde las células en estado 1 se colorean en azul y las que están en estado 0 en amarillo.
© BioMates, 2003