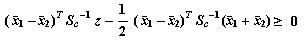
Análisis discriminante
Dos poblaciones normales bivariantes
Se dispone del siguiente conjunto de m pares ordenados que representan observaciones realizadas sobre individuos de una cierta población:
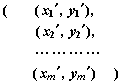
La población en cuestión está formada a su vez por dos subpoblaciones o
clases y se quiere saber a cuál de ellas pertenece cada una de las observaciones
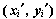 anteriores.
anteriores.
Para realizar esta asignación se obtienen sendas muestras sobre los individuos de los que se sabe con certeza a qué clase pertenecen; así se registran n1 observaciones en la primera subpoblación y n2 en la segunda, almacenando los datos en la siguiente matriz de orden (n1+n2)×3
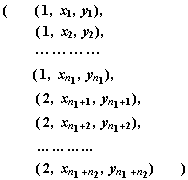
El procedimiento exige que se verifiquen las siguientes condiciones:
- Las subpoblaciones tienen distribución normal bivariante, de medias distintas y matrices de covariazas iguales.
- Las dos muestras han sido realizadas aleatoriamente.
- Las probabilidades a priori de que un individuo pertenezca a una u otra clase son iguales: p1=p2=0.5 .
- Los costes por cometer un error en la clasificación de un nuevo individuo son iguales, tanto si se clasifica en la clase 1 siendo de la clase 2, como si se clasifica en la clase 2 siendo de la 1. En un contexto médico esto es irreal; no tiene el mismo coste (en calidad de vida, moral o económico) diagnosticar un paciente como sano cuando está enfermo que enfermo cuando está sano.
- Los tamaños muestrales deben ser tales que
4
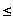 n1+n2.
En particular, este programa exige
2<n1 y 2<n2.
n1+n2.
En particular, este programa exige
2<n1 y 2<n2.
Puesto que en las situaciones reales no se conocen ni las medias ni la matriz de covarianzas común de las subpoblaciones, es necesario estimarlas.
Los estimadores de las medias son:
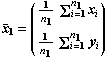
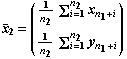
El estimador de la matriz de covarianzas se obtiene combinando (Sc) las matrices de seudo-covarianzas muestrales de cada clase (S1 y S2):
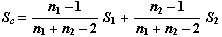
Dada una nueva observación 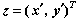 que queremos
discriminar como perteneciente a una de las dos clases, se sigue la siguiente regla:
que queremos
discriminar como perteneciente a una de las dos clases, se sigue la siguiente regla:
Se asignaráa la clase 1 si
y a la clase 2 en caso contrario.
La expresión a la izquierda del símbolo de desigualdad se puede representar de la forma lineal ax' +by' +c, lo que significa que ambas clases quedan separadas en el plano por una recta.
Se les ha extraído muestras sanguíneas a un total de 75 mujeres, 45 de las cuales eran portadoras de hemofilia. En cada muestra se han realizado las mediciones de dos variables, cuyas transformaciones logarítmicas se reflejan a continuación:
Se desea construir una función de discriminación que ayude a detectar posibles portadoras de hemofilia. Construida ésta, se quiere decidir si el siguiente grupo de mujeres a quienes se les ha extraído la muestra sanguínea son o no portadoras:
Clase 1: mujeres no portadoras Clase 2: mujeres portadoras log10(actividad AHF) log10(antígeno AHF) log10(actividad AHF) log10(antígeno AHF) -0.0056 -0.1657 -0.3478 0.1151 -0.1698 -0.1585 -0.3618 -0.2008 -0.3469 -0.1879 -0.4986 -0.086 -0.0894 0.0064 -0.5015 -0.2984 -0.1679 0.0713 -0.1326 0.0097 -0.0836 0.0106 -0.6911 -0.339 ... ... ... ...
log10(actividad AHF) log10(antígeno AHF) -0.112 -0.279 -0.059 -0.068 0.064 0.012 -0.043 -0.052 -0.05 -0.098 ... ... Aunque existen contrastes más objetivos para comprobarlo, los resultados del programa nos sugieren que las medias de ambas clases son diferentes, así como que las matrices de covarianzas (S1 y S2) son iguales, razones que hacen pertinente el uso del procedimiento de discriminación descrito. Los nuevos individuos quedan todos clasificados como pertenecientes a la clase 1 de mujeres no portadoras de hemofilia. El gráfico adjunto ayuda a visualizar el problema.
(Fuente: B.N. Bouma. et al.(1975) Evaluation of the detection rate of hemophilia carriers. Statistical Methods for Clinical Decision Making, 7(2): 339-350.)
© BioMates, 2000-2003