Supongamos una muestra de tamaño n sobre una población multivariante de dimensión 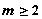, cuyos datos se disponen en una matriz de n filas y m columnas de la forma

.

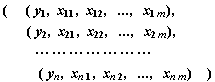Entendemos por población multivariante de dimensión m aquella en la que a cada individuo muestral se le observan exactamente m características o variables.

Podemos estar interesados en cada una de las m variables de forma independiente, en cuyo caso no necesitaremos el diagrama de dispersión. Pero lo más común en este tipo de muestras es estudiar si unas variables se relacionan con otras de algún modo, o si existe dependencia entre ellas.

En un diagrama de dispersión se escogen dos variables distintas entre las m posibles, numeradas por a y b, tales que

,

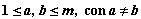Si los puntos forman una nube más o menos amorfa, podemos suponer que ambas variables no se interrelacionan, o lo que es lo mismo, el conocimiento de una no aporta información sobre la otra. Pero si ambas variables tienen un patrón de comportamiento conjunto, esto se verá en el diagrama de dispersión. El siguiente ejemplo pretende dar luz sobre lo recién comentado.

A continuación se transcribe una muestra simulada de tamaño 12 en la que a cada individuo muestral se le midieron 3 variables.

Variable 1	Variable 2	Variable 3
102	32	5.0
220	75	5.8
300	115	5.3
210	81	5.8
180	60	5.8
260	83	5.2
117	40	5.4
200	49	5.9
143	60	5.6
97	39	5.2
261	99	5.4
220	60	5.5

En la fase exploratoria se quiere obtener una apreciación sobre cómo se relacionan estas tres variables entre sí.

El diagrama de dispersión de las dos primeras variables sugiere una relación lineal y positiva entre ambas; ya que al aumentar una lo hace también la otra y de forma proporcional. Haciendo a = 1 y b = 3, tomando la primera y la tercera, parece que el comportamiento es del tipo cuadrático; la tercera variable va aumentando conforme lo hace la primera, pero luego disminuye mientras la otra sigue aumentando. Finalmente, interprete el lector lo que ocurre cuando a = 2 y b = 3.