Regresión
Regresión Lineal Simple (Recta de Regresión)
El problema de la regresión lineal simple entre dos variables X y Y se reduce a calcular la recta de regresión que mejor represente su distribución conjunta. Los datos se presentan como una matriz de dos columnas:
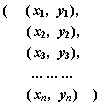
Se pretende ajustar un modelo de la forma
- La variable respuesta yi depende de la variable explicativa xi de forma lineal (con pendiente a y ordenada en origen b), más un factor residual aleatorio ei.
- Los residuos tienen distribución normal de media 0 y varianza
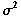 desconocida.
desconocida. - Estos factores aleatorios son independientes entre sí.
Los parámetros de la recta de regresión, a y b, se calculan siguiendo el criterio de los mínimos cuadrados, lo que lleva a los siguientes resultados:
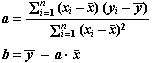
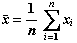
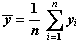
La varianza residual 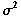 es desconocida, siendo su estimador
insesgado
es desconocida, siendo su estimador
insesgado
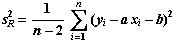
Definiendo el coeficiente de correlación como
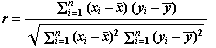 ,
,- Si r es próximo a -1: el ajuste es aceptablemente bueno, distribuyéndose las observaciones (xi, yi) alrededor de una recta de pendiente negativa.
- Si r es próximo a 0: el ajuste no es aceptable, indicando que no existe relación lineal entre las variables.
- Si r es próximo a +1: el ajuste es aceptablemente bueno, distribuyéndose las observaciones (xi, yi) alrededor de una recta de pendiente positiva.
El contraste de independencia entre las variables es más objetivo que la simple observación del coeficiente de correlación r. Así se plantea comprobar si los datos observados corroboran o no la hipótesis nula:
H0: "la variable explicativa X no influye en la respuesta Y".frente a la alternativa:
H1: "la variable explicativa X influye linealmente en la respuesta Y".Mediante el estadístico de contraste
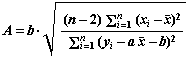
Se dispone de los datos de ocho anestesias de diferente duración, efectuadas con un anestésico volátil y del tiempo en que se restablece la conciencia suficiente como para contar hacia atrás desde un número determinado sin error:
Duración
anestesia (min)Duración
despertar (min)150 13 127 16 160 21 210 20 250 16 130 13 60 12 55 14 Se intenta probar la hipótesis de que la duración del despertar no está influida por la de la anestesia.
El coeficiente de correlación para esta muestra es de 0.562231, a medio camino entre el 0 y el 1, no permitiendo dar una respuesta segura sobre el contraste; en cambio, el estadístico A toma un valor de 1.66531, del que se puede deducir que la hipótesis no puede rechazarse al nivel del 5%; en conclusión, no hay indicios de que la duración del despertar esté linealmente relacionada con el tiempo de duración de la anestesia. Si se hubiese rechazado la hipótesis de independencia, se podrían ajustar los datos a la recta de ecuación
y = 0.03 x + 11.62, siendo x la duración de la anestesia e y la del despertar.(Fuente: J. Gil Cebrián (1995) Estadística no paramétrica. RA-MA, Madrid.)
© BioMates, 2000-2001